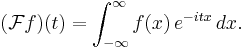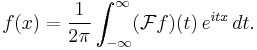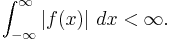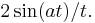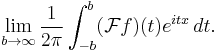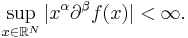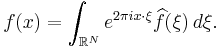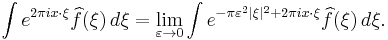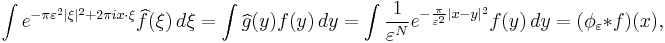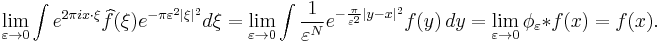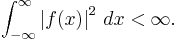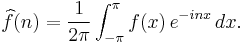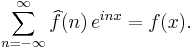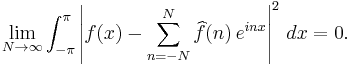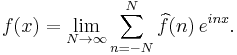Fourier inversion theorem
In mathematics, Fourier inversion recovers a function from its Fourier transform. Several different Fourier inversion theorems exist.
Sometimes the following expression is used as the definition of the Fourier transform:
Then it is asserted that
In this way, one recovers a function from its Fourier transform.
However, this way of stating a Fourier inversion theorem sweeps some more subtle issues under the carpet. One Fourier inversion theorem assumes that f is Lebesgue-integrable, i.e., the integral of its absolute value is finite:
In that case, the Fourier transform is not necessarily Lebesgue-integrable. For example, the function f(x) = 1 if −a < x < a and f(x) = 0 otherwise has Fourier transform
In such a case, Fourier inversion theorems usually investigate the convergence of the integral
By contrast, if we take f to be a tempered distribution -- a type of generalized function -- then its Fourier transform is another tempered distribution; and the Fourier inversion formula is then more simple to prove.
Contents |
Proof of the inversion theorem
First we will consider Fourier transforms of functions in the Schwartz space; these are smooth functions 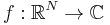 such that, for any multi-indices
such that, for any multi-indices  and
and  ,
,
These functions are clearly seen to be absolutely integrable, and the Fourier transform of a Schwarz function is also a Schwartz function. An example is the Gaussian function 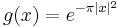 , which we will actually use in proving the inversion formula. We will use the convention that
, which we will actually use in proving the inversion formula. We will use the convention that 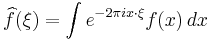 , and the claim is that for a Schwartz function
, and the claim is that for a Schwartz function  ,
,
To do this, we will need a few facts.
- For
 and
and  Schwartz functions, Fubini's theorem implies that
Schwartz functions, Fubini's theorem implies that 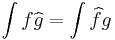 .
. - If
 and
and 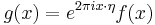 , then
, then 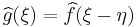 .
. - If
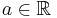 and
and 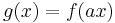 , then
, then 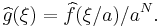
- Define
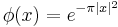 ; then
; then 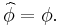
- Set
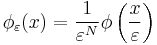 . Then with
. Then with  denoting convolution,
denoting convolution, 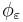 is an approximation to the identity:
is an approximation to the identity: 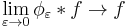 , where the convergence is uniform on bounded sets for
, where the convergence is uniform on bounded sets for  bounded and uniformly continuous and the convergence is in the p-norm for
bounded and uniformly continuous and the convergence is in the p-norm for 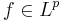 .
.
We can now prove the inversion formula. First, note that by the dominated convergence theorem
Define 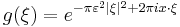 . Applying the second and then third fact from above,
. Applying the second and then third fact from above, 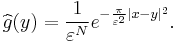 With
With 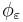 as before, we can push the Fourier transform onto
as before, we can push the Fourier transform onto  in the last integral to get
in the last integral to get
the convolution of ƒ with an approximate identity. Hence by the last fact
This establishes that the Fourier transform is an invertible map of the Schwartz space to itself. In particular, it is an isometry in the 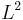 norm, and Schwartz functions are dense in
norm, and Schwartz functions are dense in 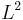 . The Fourier transform and its inverse then extend to unitary operators
. The Fourier transform and its inverse then extend to unitary operators 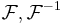 on all of
on all of 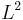 for which
for which 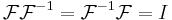 , with
, with  the identity map.
the identity map.
While the integral defining the Fourier transform or its inverse may not make sense for general 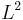 functions, one can always integrate over a symmetric rectangle and take the limits as its length tends to infinity. What one is really doing here is taking an increasing sequence
functions, one can always integrate over a symmetric rectangle and take the limits as its length tends to infinity. What one is really doing here is taking an increasing sequence 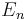 of relatively compact sets growing to
of relatively compact sets growing to 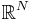 , and taking the limit of
, and taking the limit of 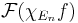 , where
, where 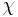 denotes the indicator function of a set. Since
denotes the indicator function of a set. Since 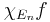 is compactly supported, the integral defining its Fourier transform exists. But clearly
is compactly supported, the integral defining its Fourier transform exists. But clearly 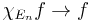 in
in 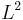 , hence
, hence 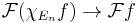 as well.
as well.
Fourier transforms of square-integrable functions
Via the Plancherel theorem, one can also define the Fourier transform of a square-integrable function, i.e., one satisfying
Then the Fourier transform is another quadratically integrable function.
In case f is a square-integrable periodic function on the interval ![[-\pi, \pi]](/2012-wikipedia_en_all_nopic_01_2012/I/911bebeafbf3d4845e122edfc4f667f8.png) , it has a Fourier series whose coefficients are
, it has a Fourier series whose coefficients are
The Fourier inversion theorem might then say that
What kind of convergence is right? "Convergence in mean square" can be proved fairly easily:
What about convergence almost everywhere? That would say that if f is square-integrable, then for "almost every" value of x between 0 and 2π we have
This was not proved until 1966 in (Carleson, 1966).
For strictly finitary discrete Fourier transforms, these delicate questions of convergence are avoided.
See also
References
- G.B. Folland, Introduction to Partial Differential Equations, 2nd ed, Princeton University Press, 1995.
- Lennart Carleson (1966). On the convergence and growth of partial sums of Fourier series. Acta Math. 116, 135–157.